浅析山区输电线路悬垂线夹的磨损

 　高压输电线路是连接变电站、传输电力的通道，是电网的重要组成部分。从城市规划和少占农田耕地考虑，往往将这些线路架设到山区或丘陵地带。目前北京供电局输电处负责运行的3 654km线路中，位于山区或丘陵段的线路有563 km，比例为15．4％。处于山顶、风口和微地形段的线路常年受风的作用，线路联接各部件（称金具）易反复摇动，造成导、地线和金具的磨损断裂，酿成线路事故。从多年的运行情况看，直线塔用于悬挂导、地线的悬垂线夹（以下简称线夹，见图1）磨损比较突出，近10年共发生8起该类事故，而且有逐年增加的趋势。处于什么地形和铁塔其线夹易磨损，磨损和哪些因素有关，一直是线路运行维护部门十分关注的问题。

1　磨损值的测量及分析
　　针对山区线路线夹磨损的问题，从1996年起采取了检修人员登塔打开线夹检查磨损情况的措施。全年有计划、有重点的对53条线路进行了登杆塔检查，共发现磨损线夹425个，其中7处磨损严重。在检查的53条线路中，以处于北京西南的220 kV吕村变电站至西北的聂各庄变电站两条220 kV线路（以下简称吕聂一、二回）磨损最严重，两条线路共换下36个磨损线夹（集中于14基杆塔上），本文以该两条线路为例进行重点分析。

    吕聂一、吕聂二线路两路同塔并架（见图2），全线共有94基塔，路径走向基本位于北京的西部和北部山区。磨损线夹换下后及时进行了测量（测量值略）。针对36个磨损线夹分析如下：

　
1．1　磨损线夹的地形分布情况
　　线路在吕村站出口段基本是丘陵地区，沿线地形情况及磨损塔位分布如下：
   （1）位于丘陵段（1～10号）没有磨损；

   （2）位于山区段（11～92号）有14基磨损；　　

   （3）位于平原段（93～94号）没有磨损。
1．2　磨损线夹的塔号
　　导线磨损的基数：6基（56、62、78、79、85、89号）；
　　地线磨损的基数：14基（40、47、56、57、62、70、71、72、74、78、79、85、87、89号）。
　　由线夹磨损的塔号可看出地线磨损线夹的塔号全部包括了导线线夹的塔号，从而可得到这样的结论：导线线夹有磨损则地线线夹一定被磨损。

1．3　磨损量分析
　　在36个被磨线夹中，磨损最严重的磨掉7．5mm（一回85号地线），磨损率为44．1％；磨损最轻的磨掉0．2 mm（一回56号2线上和地线），磨损率为1．1％。导线线夹磨损最严重达4．8 mm（一回78号2线上），磨损率为26．7％；地线线夹磨损最严重的达7．5 mm（一回85号），磨损率为44．1％。由此可见，地线线夹的磨损率大于导线。

1．4　磨损值计算
　　导、地线线夹磨损分布在14基塔、36个线夹上，共有90个磨损点，因数据较多，不便于比较，很难看出线夹被磨损的规律性；特别是导线线夹，同一相线有上、下两个分裂线线夹，每个线夹磨损值又分为左右两个轴。为便于比较，先计算出每条线所在线夹左、右轴的磨损平均值，进而计算出1、2、3线线夹（即每相线）的磨损平均值，再计算出3条线（即每回线）的磨损平均值，计算的中间结果略。
1．4．1　导线每相线的线夹磨损
　　1、2、3线线夹磨损平均值计算结果分别见表1和表2。

　　
　　由表1和表2可见，1、2、3线线夹的磨损平均值基本服从依次降低的规律。
1．4．2　导线每回线线夹及地线线夹的磨损　　

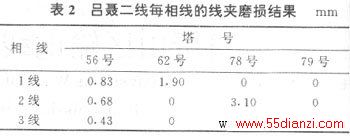
    一回和二回线线夹磨损平均值以吕聂一线磨损值由大到小排列，见表3，地线线夹磨损平均值（由大到小排序）见表4。

　　
　　由表3、表4可见，导线和地线线夹磨损的塔号排序除个别塔号移动几位外，其大体趋势相同（都是85号最严重，56号较轻）。
1．5　定性分析磨损情况　　
　　线夹的磨损与其受力有主要关系，受上拔力或下压力很小都会产生磨损，而受力大小完全由地形决定。从设计角度考虑，在排定塔位时应尽量避免出现较小的垂直档距，即对山谷中的塔位和大跨越的塔位要特别注意。从运行经验看，处在连续下山的塔位线夹易磨损。针对吕聂一、二线发生的14基塔的磨损，查阅了该线路的设计平断面图，发现有如下规律：

（1）连续下山段中的直线塔的线夹易磨损。　

  　（2）相邻两基塔高出本塔（即可能受上拔力，如72、79号）则易磨损。
　　（3）处于山头的塔（受下压）也会发生线夹磨　　损（如56、71号）。

2  磨损线夹受力计算

    为找出磨损线夹与其受力（上拔或下压）的量值关系，可分别计算出14基塔的导、地线受力数据。

2．1　导线受力计算
　　上拔力计算公式为：
TB＝｛（L1＋L2）g／2＋σ［（±（h1cosφ1）／L1±　　（h2cosφ2）／L2）］｝S           （1）

式中  　L1——上拔力杆塔一侧的档距，m；
        L2——上拔力杆塔另一侧的档距，m；

        g——导线的比载，kg／（mm2·m）； 
     σ——导线低温时的应力，Pa；
       h1——杆塔与一侧杆塔的高差，m；　

     　h2——杆塔与另一侧杆塔的高差，m；
     cosφ1——杆塔与一侧杆塔的高差角，（°）；

     cosφ2——杆塔与另一侧杆塔的高差角，（°）；

      S——导线截面积，mm2；
      TB——杆塔所受上拔力，N。
　　当h／L＞0．1时，按大高差情况计算，此时应考虑cosφ。
例：计算78号塔的上拔力。查设计图纸得：

      S＝335 mm2；　σ＝61．29 MPa；
      h1＝39 m；h2＝59 m；
      L1＝417 m；L2＝710 m；
      g1＝3．331×10－3 kg／（mm2·m）；

      cosφ1＝cosφ2＝1。
      上拔力：TB＝6．37（kN）
　　同理可计算出其它几基塔的上拔力，按上拔力由大到小排序见表5。

　　
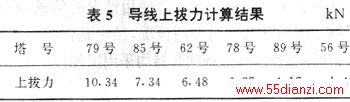
　　注：表中负数说明该塔是受下压力。
2．2　地线受力计算
　　经计算，地线所受上拔力由大至小排序，见表6。
    由导、地线上拔力数据可得出以下几条规律：　

 　（1）发生线夹磨损的塔位大部分受上拔力，这和人们以往对磨损机理的认识是吻合的。　

 　（2）导线、地线上拔力的塔号排序是一致的，这说明上拔力的大小主要和地势有关，同时也验证了计算的正确性。
　　（3）上拔力的排序和1．4．2条中的磨损量的排序比较可见其总的趋势是一致的。56号塔无论磨损量还是受力都排在最后，但磨损量85号最严重，而受力79号最严重。经查阅事故记录，1995年曾对79号、地线夹进行了更换，所以仍可说79号的磨损也最严重。

[1] [2]  下一页