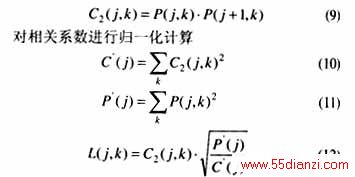(1)对测量信号进行小波变换,采用具有反对称结构的二次样条小波,因为这种小波能突出脉冲型信号。由于采用非正交的小波基,不能利用Mallat 算法,用à Trous快速算法进行各尺度的分解和最后的重构。这种算法的优点在于小波的分解能保持平移不变性,从而可以度量小波系数沿尺度的衰减性。设数据的个数为
N,则小波分解的最大尺度数
J为2
J≤N。
(2)Teager 能量算子用于计算信号的局部强化能量,对离散信号x(n),其Teager函数x'(n)定义为

k=1,2,…,N;W(j,k)为信号在第
j尺度上第
k个小波系数。
(3)计算相邻两尺度的相关系数,其相关系数矩阵的计算采用如下公式
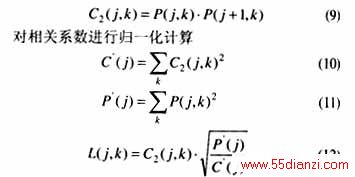
将得到的经归一化计算的相关系数L(j,k)和尺度j及j+1的小波系数比较。设在某尺度j
1的小波系数中,当某一点L(j
1,k
1)
≥P(j
1,k
1)时,认为该点对应于奇异点。在新的向量
M(
j,
k)中保留该点,即M(j
1,k
1)=1,这使得信号的奇异点能量得以保留。M即为相应尺度j
1的屏蔽滤波器。
(4)对得到的相邻两个屏蔽滤器进行逻辑“与”运算。
若得到准确的空间屏蔽滤器,其关键在于如何削弱噪声而同时增强局放信号。由于白噪声的小波系数随尺度的衰减幅度大于局放信号,在前两个尺度小波系数较大的噪声信号在后两个尺度将变得很小,而局放信号随尺度衰减不大或者保持不变。噪声信号大部分集中在较细的尺度上,尤其是最细的尺度,而在较大的尺度上奇异点的定位性又很差,因此选择尺度2、3、4上的屏蔽滤波器进行计算。对尺度2和尺度3得到的屏蔽滤波器和由尺度3及尺度4得到的屏蔽滤波器进行逻辑“与”运算。即只取在三个尺度都保持最大的信号奇异点,这样就能有效滤除噪声的干扰。
(5)由于à Trous算法是对滤波器在不同尺度上进行插值补零运算得到新的滤波器再进行卷积
运算,因此对屏蔽滤波器在不同尺度运算也要进行相应的扩展,使得最大限度的保留奇异点信号的能量。
(6)对得到的屏蔽滤波器和不同尺度小波系数相乘,得到新的小波系数,重构后得到局部放电脉冲。
传统的去噪方法都是假设随机噪声是零均值和固定方差的,在此假设基础上对信号去噪不能保证干净的滤除噪声,而本文提出的方法不要求噪声一定是白的,因此该方法有很强的鲁棒性。
4 试验
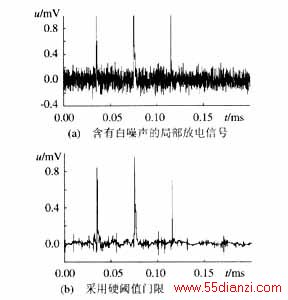
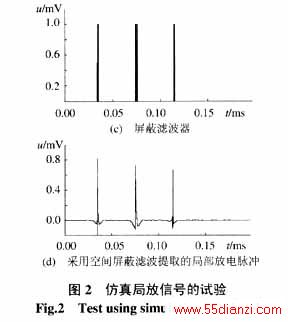
图2为仿真信号的脉冲提取过程。局部放电信号采用指数衰减信号来模拟,在图2(a)的信号由3个时间常数为0.5ms的指数衰减信号和均值为零,方差为1的白噪声信号叠加而成。图2(b)为采用传统的门限方法去噪后的结果。从图中可以看出,在信号中仍然保留了部分噪声,还需要进一步处理,而进一步的处理就会进一步降低局放信号的幅值和能量,这不利于后续的信号分析。图2(c)为在2、3、4尺度上得到的屏蔽滤波器。由图2(c)可见,屏蔽滤波器的位置正是局部放电脉冲的位置,该屏蔽滤波器检测到了所有的信号奇异点。图2(d)为利用屏蔽滤波器提取到的小波系数重构后得到的局放信号。由图可见,获得的信号最大限度地抑制了噪声,并保存了局部放电信号的大部分的幅值和能量,这有利于后续的局部放电信号分析和寿命预测。
为了考察该算法对实际信号的有效性,采用实验室的线棒放电信号来验证。由于实验室的线棒放电噪声干扰小,在未加噪声的情况下易于识别,因此可以用来验证算法的准确性。
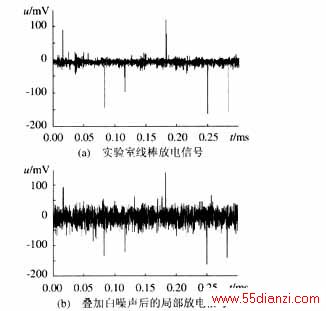
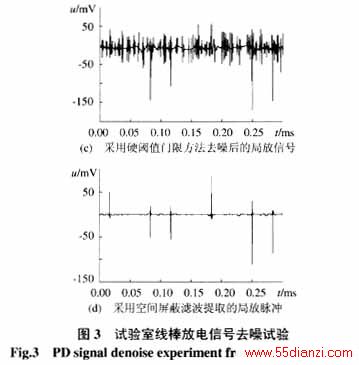
图3(a)为实测的线棒放电数据。从中可以看出,该信号包含有6个较大的放电脉冲,其中包括正脉冲和负脉冲。图3(b)为叠加白噪声后的信号。图3(c)为采用db4小波和硬门限方法去噪后的信号,从图中可以看出,在信噪比较低的情况下其滤波效果很差,难以分辨局放脉冲和噪声。采用改进的屏蔽滤波算法得到的局放信号显示在图3(d)中。从试验可以看出,该算法能准确判定局部放电信号的位置,并检测出了所有的局放脉冲,经重构后的信号保留了局放信号的大部分能量。
5 结论
本文给出了利用改进的空间屏蔽滤波器从含有白噪声的信号中提取局部放电脉冲的新算法。从上面的算法分析和试验测试可以看出,采用Teager能量算子能强化信号的奇异点,有利于后续的屏蔽滤波器设置;利用小波系数在三个尺度上的变化形成最终的空间屏蔽滤波器,保证了奇异点的准确性。
上一页 [1] [2]
本文关键字:空间 电脉冲 电工技术,电工技术 - 电工技术