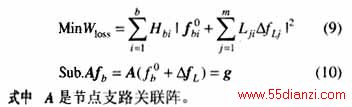
因A△fL=0，且
。若固定节点注入电流，则g=g0 。原问题转化为一无约束二次规划问题。
系统优化目标Wloss 的充分条件为
设系统存在m个独立回路，则对式(9)求偏微分可得
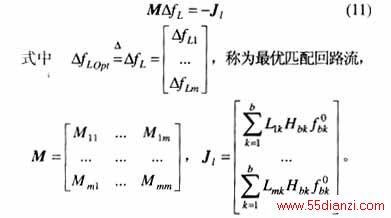
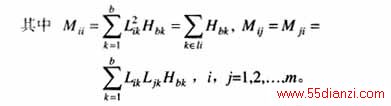
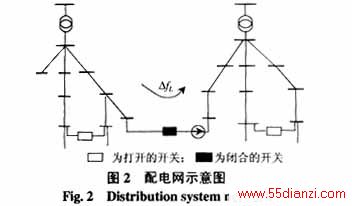
需要指出的是：当系统是单环网且优化目标是系统网损最小时，式(11)与文[2]得出的结论是等价的。显然，用这种公式推出来的结果只满足KCL定理而不满足KVL定理。但我们是模拟逼近回路断开后的情况，而回路断开后本来就不存在KVL约束，所以它作为一种带误差的优化方法是可以接受的。
式(11)中M阵具有如下性质：
（1）Mii>Mij,i!=j, 所以它有很好的数值稳定性；
（2）M是一个定常阵，而且是高度稀疏的，因而可以采用稀疏矩阵技术求解。
以上的模型可以很容易地扩展到三相模型。
3.4 回路开断顺序的确定
定义3：若任一回路k上叠加最优匹配流后的电流最小的支路残留电流为δLK ，δLk 定义为回路k的残留电流，δL 定义为回路的残留电流矢量。
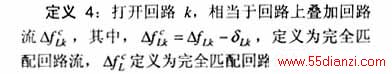
电网中可能存在有的回路的最优开断支路在多条回路的共同支路集上。此时，不能单纯按断开回路的最优开断支路来打开回路。否则会导致有的回路没有被打开的情况，所以如何确定回路的开断顺序是很重要的。
为了易于理解，本文利用两个回路的最优开断支路在共同支路集的情况来解释该算法。设回路k和l的最优开断支路在共同的支路集上，若先开断回路k，则打开回路l的支路时要选择它们共同支路集以外的残留电流最小的支路；反之亦然。 设第一种方案的回路k和回路l的完全匹配流分别
认为其他回路的完全匹配流保持不变，则根据式(9)，这两种方案的目标差值可用下式估计：
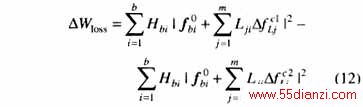
若△Wolss<0 ,则选择第一种方案，否则，选择第二种方案。由于式(12)中的变量都是已知量，所以△Wolss 的计算量是很小的。
4 网络重构算法
网络重构算法的分为两步：
第一步称为初始优化。首先，合上所有联络开关，形成多环网系统。然后找出所有的独立回路，计算最优匹配回路流。根据式(15)确定回路开断的顺序。经过第一步的计算后，系统得到一个优化后的辐射状电网。此时，系统已得到很大的优化，并且联络开关两端的电压已很接近。
第二步称为寻优迭代。这一步的任务就是通过转移联络开关两端的局部负荷来进一步优化网络。由于联络开关两端的电压已很接近，所以，它们之间的负荷转移可以用一个反向的回路电流来近似模拟。对于辐射电网的负荷转移，也可以用最优匹配回路流来模拟。其计算方法和公式与环网的最优匹配回路流是一样的。
初始优化的算法如下：
（1）初始化系统,合上所有联络开关，形成多环网系统；
（2）计算三相多环网潮流；
（3）计算最优匹配回路流△fLOpt ；
（4）计算各回路的残留电流δL
本文关键字：网络 电工技术，电工技术 - 电工技术
