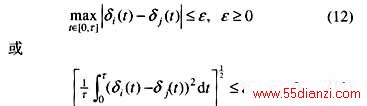
就认为是同调的。如果一群发电机两两同调，则这群发电机是同调的。
对每一个动态场景sÎS1，采用式(12)或(13)所定义的同调性准则，得到描述各台发电机之间的同调性的矩阵C
对于一个nG机系统，C是nG×nG的对称方阵。元素C (i, j)表示发电机i和j的同调性，等于1表示同调，等于0则表示不同调。
同调分群即是对发电机集合NG进行划分，使分群数最小而每一个机群中的各发电机都是同调的，是一个组合优化问题，组合数随C的阶数指数增长，宜于采用启发式搜索算法。
本文采用一种简单的随机搜索算法。在算法中引入电气距离指标，在最小分群的同时使同一机群中的各发电机间的电气距离尽可能近，从而使不同机群的电气距离尽可能远，以避免电气距离接近的发电机分在不同机群中。
在每一个同调机群中，取额定有功功率最大的发电机作为代表，组成配置地点的候选集合NC。
3.4 配置地点选择
设候选集合NC由nC台发电机组成，nT是给定的转子角测量装置的数目，由式(7)、(8)所定义的最优化问题转化为在nC台候选发电机中选取nT台使其转子角响应的信息含量最大。如果nC小于或等于nT，NC就是解，但是nC通常大于nT。当nC大于nT时，以Gramian行列式作为信息含量的表征进行求解。
从转子角矩阵R中取出对应于NC的列构成候选集合的转子角矩阵RC
的主对角元素表征了各候选发电机转子角的整体响应，非对角元素则表征了转子角响应之间的相关性。
将Gramian行列式作为信息含量的表征[7]，前述nC选nT的问题转化为从RC中选取nT列使相应的m×nT阶子矩阵的Gramian行列式值最大。总共有
种组合。随着组合数的增加，穷尽式搜索对应的计算量和耗时迅速增多，甚至不可行。
Tabu搜索通过记录搜索历史对搜索过程进行控制以避开局部最优解，是一种高效的启发式搜索技术，适合于解决组合优化问题。本文采用文献[8]所提出的Tabu搜索算法，其主要的思路是：① 随机选取nT 个列作为初始解；② 用lIN和lOUT分别表示当前nT 个选中列与
个未选中列，从lIN和lOUT中各取一列互换，进行nT×（）次交换，若产生最优解的交换不是Tabu表的内容，接受，否则，不接受；③ 把在每次迭代中产生最优解的交换存入Tabu表；④ 终止准则是迭代超过预先设定的最大迭代次数。
一个动态场景sÎS1就对应着一组配置地点，共有ns1组（ns1是压缩场景集的场景数）。如果取ns1组配置地点的并集作为最终的配置地点，所需的装置数目往往超过给定值 nT。本文采用一种基于概率的方法，令
Ti表示对应场景i发电机j是否被选中；等于1表示是，等于0则表示否；Pj表示发电机j是最终的配置地点的概率。
Pj 反映了发电机j对多动态场景的适应性，值越大，适应性就越强，因此，将概率值最大的nT台发电机作为最终的配置地点。
4 实例仿真
4.1 数字仿真
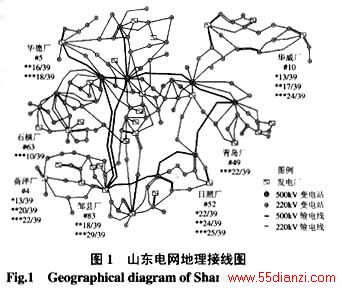
在仿真的2002年山东电网中，有84台发电机、362个节点、406条交流线和240个负荷，500 kV及220 kV电网的地理接线如图1所示。计划为山东电网设计一种暂态稳定紧急控制方案，监视发电机转子角并预测其发展，并据此决定是否启动紧急控制措施以保持系统的暂态稳定性。作为方案的重要组成部分，需要研究在投资额给定（即基于GPS的转子角测量装置的数目给定）条件下的最优配置问题。
采用电力系统分析综合程序PSASP 6.1进行数字仿真。考虑4个稳态运行点对应4种负荷水平，分别是：105%、100%、95%以及90%的基本负荷水平。对每一个稳态运行点各仿真196个线路及母线短路故障，包括：所有的10条500kV线路、根据运行经验选定的3条东部地区的220kV线路和一个母线。故障类型包括单相接地、两相相间、两相接地以及三相接地短路；对线路故障，以线路两端和中间代表不同的故障地点。因为500kV和220kV线路多采用单相重合闸技术，所以计及了重合于永久性单相接地故障的情况。总共仿真了784[=(10×15+3×15+1)×4] 个动态场景。每一个场景的时间窗是5s，积分步长是0.01s，对应着501×84的发电机转子角矩阵R，其中，501和84分别是转子角的采样数和发电机数。784个动态场景中的780个是稳定的，4个是不稳定的。
4.2 动态场景的聚类
将每一个稳定的动态场景表示成矩阵
本文关键字：测量 电工技术，电工技术 - 电工技术
