1 FFT 测频
信号x( t) 经过数字化采样后为x( n) ,n = 0,1,2,…,N - 1 ,为对其进行频谱分析,进行离散傅里叶变换( DFT) ,将信号从时域转换到频域,如式( 2)所示:
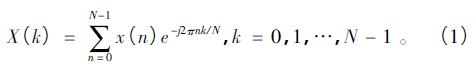
DFT 实现时采用的快速算法即是FFT,经FFT处理后,信号的频率分辨率为:
式中,fs为采样率,设信号的时宽为T%20,则信号的点数为T%20×%20fs,信号的频率分辨率可表示为:
可见,FFT 测频的频率分辨率只与信 号时宽有关,根据谱线的最大值来换算信号的频率,如果信号的频率正好落在一根谱线上,得到的频率测量结果是准确的,而在多数情况下,信号频率落在两根谱线之间,由最大值谱线位置反映的频率不再准确,最大测频误差为Δf /2 。
脉冲是雷达最常采用的信号形式,根据需要,雷达有时会采用脉内带调制的信号类型,例如相位编码、线性调频等,对于此类复杂信号可采用各种信号处理方法将其转化为普通正弦波信号,因此正弦波脉冲的测频方法具有通用性。根据上文分析结果,对于时宽较长的脉冲,采用FFT 测频法易于实现较高测频精度,满足设备指标要求。但是对于短脉冲,例如一个0. 2 μs宽的脉冲,根据式( 3) ,理论能达到的测频精度只有2. 5 MHz,难以满足侦察要求。
2 补零技术
补零是指在进行FFT 运算之前在时域数据的尾部添加一些零,并使总的时域数据点数保持为2 的幂次方。由于补零不增加任何新的信息,所以并不改变频谱形状和频率分辨率,补零只是在原始点数的FFT 结果中内插了一些频率分量。对于点数较少的FFT 结果,在大多数情况下,从中找到峰值比较困难,也很难观察到频谱的细微结构。而补零之后,功率谱的峰值位置可以较清晰的显露出来,有助于提高对主瓣峰值频率分量进行精确定位的能力,由此提高测频精度。
补零技术的缺点是额外增加了处理量,补零越多,处理时间也就越长。此外,对于存在噪声的情况,补零也不能改善信噪比,存在频谱峰值点定位错误的可能,造成测频误差增大。
3 插值FFT 测频方法分析
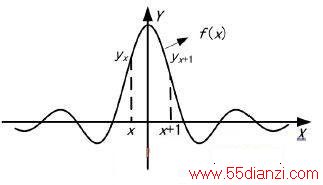
图1 矩形窗频谱函数
在图1 中插值频率校正即求出矩形窗谱主瓣中心与相邻谱线的横坐标差,对于谱线位置x 、x + 1 ,其矩形窗谱函数为sinc 函数,表示为f( x) ,频谱值为yx 、yx+1,矩形窗谱函数和频谱值已知,可构成一方程如下:
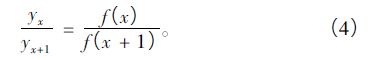
在图1 中, sinc 函数以峰值横坐标为零点 ,频率修正值δ = - x ,只要根据式( 4) 求解出x ,即可得到频率修正值。
对矩形窗谱函数归一化,求模可得:

带入式( 4) ,得到:
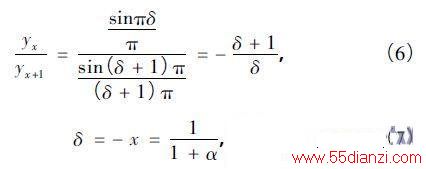
式中 ,α = yx /yx+1 。实际应用中,已知FFT 谱峰最大值位置k1,相邻次大值位置k2,频率分辨率Δf ,利用修正频率值校正频率可得:
当k2 = k1 + 1 时,取加号; k2 = k1 - 1 时,取减号。
3. 2 噪声条件下性能分析
以上对插值FFT 频率估计法进行了理论分析,实际应用中,不可避免的会有背景噪声,本小节将在加性高斯白噪声背景下,通过仿真分析插值FFT 频率估计法的性能。
设定仿真参数,信号采样率fs为1 280 MHz,脉冲宽度0. 2 μs,频率分别设f1为102. 4 MHz,f2为100. 4 MHz,按照10 dB信噪比加入高斯白噪声。
以信号频率f1进行仿真,连续测频1 000次,仿真结果如图2 所示。由图可知,最大测频误差不超过300 kHz。

图2 测频误差变化图
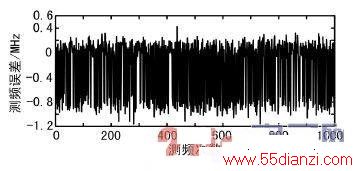
以信号频率f2进行仿真,连续测频1 000次,仿真结果如图3 所示。由图3 可知,最大测频误差超过1 MHz。
本文关键字:工程 振荡器-波形-信号电路,单元电路 - 振荡器-波形-信号电路