其中ε 是时钟误差。
设φ(i)是第i个码元间隔的相位,即:
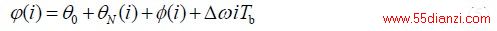
其中,φ (i)是第i个码元间隔差分编码后的相位, θ 0是初始相位差,θN (i)为噪声引起的相移, ΔωiTb为频偏引起的相移。
设有 K 个码元间隔参与频偏估计,由于频偏相对于码元速率缓慢变化,因此这在K 个区间内频偏视为恒定值。则设第i 个码元间隔的第j 个样点的相位为? (i, j),它与前一码元间隔相同采样时刻的差分相位为:
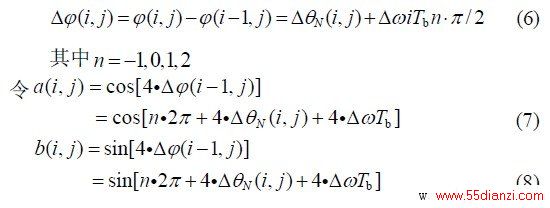
这一过程相当于去掉了调制项和初始相位的影响。
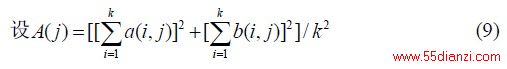
对于不同的(j 1 ≤ j ≤ M ),求出A( j)的最大值:A( j' ),则其对应的子序列即为最佳采样序列,也就是对应着最佳采样时刻。
针对最佳采样序列的差分相位先乘以2 取正切值,再取反正切除以2,即得到频偏估计。因为反正切取值为[?π /2,π /2],周期为π ,将差分相位乘以2 后就相当于在后面的运算中去掉了调制信息的影响。将频偏估计通过Kalman 滤波器进行平滑迭代,然后在参与估计的码元中对上述结果求平均,即可估计出频偏值ΔωTb.
3.2 初始相位差估计
将估计的频偏值与数字下变频后的基带信号进行复数乘法运算,得到校正后的信号,该信号中还含有收发端固有的相位差以及频偏估计不准确引起的相位偏移,除此之外还有消除频偏时引入的相位偏移。
信号传输以及通过滤波器会引起码元延迟,而频偏引起的相位偏移ΔωTb与码元位置有关,当码元延迟Δi 时,消除频偏时就会引入Δi ·ΔωTb的相移。
以上相移总和通过相位估计加以估计。
此 时, 最佳序列的各采样点相位为?(n) =θ +θN (n) +φ (n),其中,φ (n)是第n 个码元间隔差分编码后的相位,θ 是初始相位差θ 0与消除频偏时引入的固定相移之和,θ N (n)为噪声引起的相移。
当同相和正交支路都为2 电平信号时,产生的OQPSK信号有π /4 的初始相位,即φ (n) =π / 4+ n·π / 2 ,其中n = ?1,0,1, 2.对φ (n)进行如下运算:
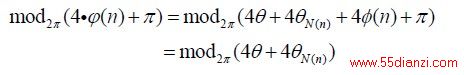
再将运算结果除以四就得到相位差的估计,但是这样估计的结果存在四维相位模糊度,要通过差分编译码消除。将得到的相位估计值再次与校正过频偏的信号进行复数乘法消除相位差的影响。以上过程如图6 所示。

图6 相位差估计过程
最后,将得到的I 路信号延迟一个码元间隔,与Q 路信号对齐,每两个码元间隔即为一个码元符号,由此得到解调数据。
以上算法在Matlab 中用M 函数进行仿真,用程序得以验证。
4 性能分析
在进行频偏估计时,有取反正切的运算,要使频偏值乘以2 后在取反正切时不在相位上发生混迭,要求频偏满足以下条件:
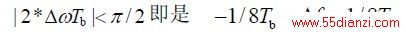
其中 Tb 为码元间隔,上式表明频偏估计范围为[-1/ 8Tb ,1/ 8Tb ].
但在噪声的影响下,实际估计会小于这一范围。这是因为相位噪声的叠加会| 2*ΔωTb |超出π /2,使得在估计时出现较大偏差。
图 7 是在不同信噪比下,理论值与仿真值的比较,两者在10?4误码率之后有大约1.5dB的差。
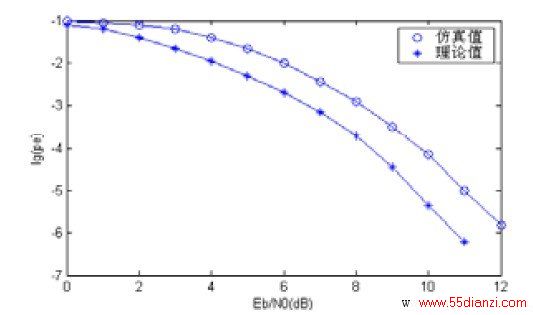
图 7 OQPSK 相干解调理论与仿真误码率比较
5 结论
本文首先介绍了FQPSK信号的构成,通过比较得到FQPSK调制方式的优点,同时指出同步技术是FQPSK 信号解调的主要任务。在此基础上,与现有成熟算法相结合,提出一种计算量小,易于实现的同步方法,它采用最佳采样点提取和差分相位算法进行信号的同步估计。计算机仿真结果表明,该方法是可行的,适合DSP实现。
本文关键字:技术 电子技术,电工技术 - 电子技术
上一篇:变容二极管的驱动技巧