根据FFT的输入数据点数N的计算式:N=fs×L,以及采样频率fs和分析窗长度L的取值,可以得到N=32。这就是说,本控制系统须做32点的FFT。
2.2 幅值补偿系数和相位补偿系数的确定
在图2中,电压源U代表来自逆变桥的输出电压,电感L和电容C构成输出LC滤波器,电流源I代表负载汲取的电流,与滤波电感L串联的电阻r是滤波电感的等效串联电阻。由图2可知,在把逆变桥看作一个比例环节的情况下,逆变器的数学模型就是由输出LC滤波器构成的二阶系统。在本系统中,L=0.552mH,r=0.3Ω,C=135μF,所以逆变器数学模型为G1(s)=3663 2/(s2+2×0.074×3663s+3663 2) (7)
它的离散化表达式为G1(z)=(0.1007z+0.09845)/(z2 -1.735z+0.9343) (8)
根据图3,可以很方便地得到幅值补偿系数modcoeff(n)和相位补偿系数phacoeff(n)。表1给出了最终的取值。
表1 补偿系数的取值
波次
幅值补偿系数(放大倍数)
相位补偿系数(角度)
基波
0.993
0.7
3次谐波
0.934
2.3
5次谐波
0.818
4.5
7次谐波
0.643
7.9
9次谐波
0.417
15.7
3 实验结果
对本文所用的控制方案进行了实验,逆变器参数为L=0.552mH,r=0.3Ω,C=135μF,开关频率f=8kHz,输出频率50Hz,幅值110V的交流电压。采用一片TI的TMS320F240定点DSP实现所有的控制功能。阻性负载参数为R=11Ω。整流型负载参数为L=0.8mH,C=2460μF,R=27Ω。
实验波形如图4,图5和图6所示。
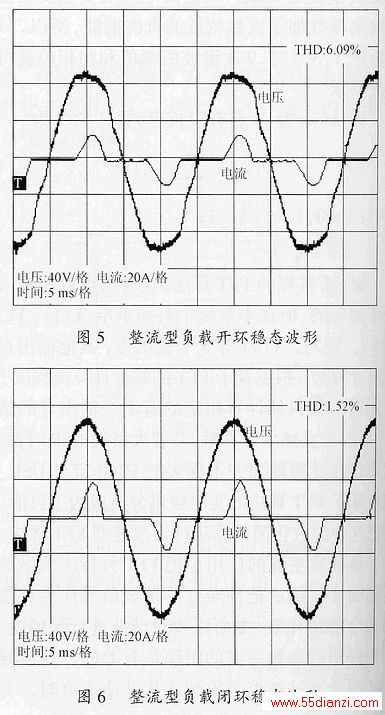
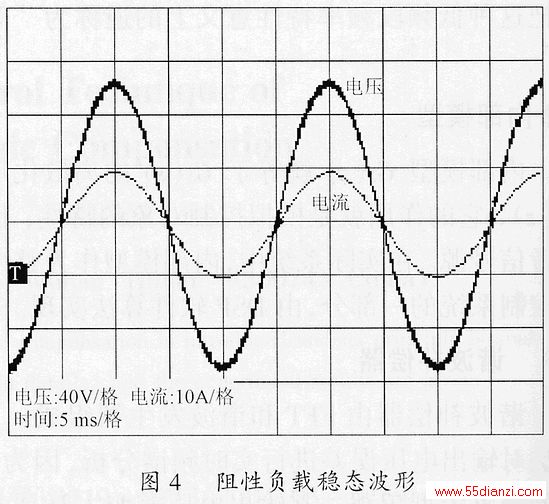
图4给出了逆变器接阻性负载的稳态输出电压和电流波形。图5及图6分别给出了逆变器在接整流型负载情况下开环稳态、闭环稳态的实验波形。可以看出开环情况下输出电压波形畸变严重,闭环以后输出电压波形有了极大的改善。
4 结语
本文采用了一种与重复控制不同的波形控制方案。实验结果表明,本文采用的改进型FFT算法大大减少了计算量,保证了在F240定点DSP上实现实时频谱分析,并且整个控制系统拥有较好的稳态性能。这说明本文采用的控制方案在理论上是正确的,实践上是可行的。而且,这种基于谐波补偿思想的控制技术还有谐波补偿器补偿系数设计简单的优点。总之,该控制方案具有较好的性能,还有一些独特的优点,有一定的实用价值。