电路工作在该情况的临界条件应满足
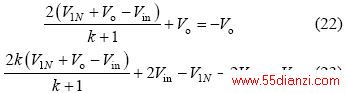
由式（22）和（23）可解得
因此，满足情况1 的条件是Vo<Vin/（1+ k）。
电路稳态工作时有
平均充电电流为
当输出电容电压为零（即输出短路）时，该谐振电路与串联谐振电路工作在输出短路时完全相同，其谐振电流为大小为
从上面的分析可以看出，V1N 是一个超越方程，解出V1N 是相当困难的，有必要研究其充电规律，找出较为理想的设计方法。
由式（2）～（25）可以看出，V 1N+1 只与谐振电容的比值有关，与谐振电容本身大小和谐振电感大小无关，因而V1N、V1N’、Z1IN’’均为Vin、Vo 和k 的函数。
故由式（24）和（27）可得如下结论：
（1）工作在该情况下的条件是Vo<Vin/（k+1）；
（2）
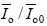与谐振电容本身大小和谐振电感大小无关，只与谐振电容的比值有关，且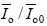为Vo/Vin 和k 的函数；当k 一定时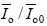，为Vo/Vin 的函数。
情况2：充电电流在正谐振半个周期内存在，在负谐振周期内充电电流为零，则有如下3 种工作模式。
模式1： Q1、Q3 导通，v2（t0）<Vo，整流二极管均截止，谐振电流i>0，充电电流io=0，等效电路如图4（a）所示。
模式2：当v2（t1）=Vo 时，整流二极管D5、D7 导通，io=i，其等效电路如图4（b）所示。
模式3：当谐振电流i（t2）<0 时，续流二极管D1、D3 导通，整流二极管截止，io=0，等效电路如图4（a）所示。
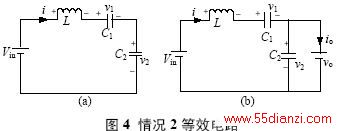
仿情况1 分析，可得如下结论：
（1）工作在该情况下的条件是Vin /（k+1） <Vo<2Vin/（k+1）；
（2）
是k 和Vo/Vin 的函数，与谐振参数本身大小无关。
情况3：充电电流在正负谐振半个周期均为零，则有如下两种工作模式
模式1：Q1、Q3 导通，v1（t0）=V1N，v2（t0）=V2N<Vo，其等效工作电路如图5 所示。
模式2：当i（t1）=0 时，进入该模式，半个谐振周期后结束，等效电路如图5 所示。
仿情况1 分析，可得如下结论：
工作在该情况下的条件是Vo>2Vin/（k+1），充电电流为零。
根据上面3 种情况得分析，可得到串并联谐振CCPS 具有如下性质：
（1）k 一定时，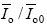
随Vo/Vin 的变化关系相同；
（2）充电电压最高可达到2Vin/（k+1） 。
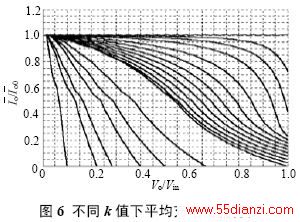
根据上面的性质，通过仿真可以得到不同k 值情况下的 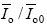随Vo/Vin 的变化曲线，如图6 所示，该图可用于谐振参数设计和调试。曲线从上到下k值依次为：0；0.02；0.05；0.1；0.2；0.3；0.4；0.5；0.6；0.7；0.8；0.9；1.0；2.0；3.0；4.0；6.0；8.0；19.0。
由图6 可得如下结论：
（1）开环控制的串并联谐振CCPS，其充电电流随着输出电压的升高而减小，平均充电电流不恒定；
（2）Vo/Vin 相同时，随着k 变大，其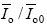越小，要提高高电压时的充电电流，就必需减小k 值；
（3）k 相同时，[IMG]/uploadpic/THESIS/2008/2/2008022916273426245D.jpg[/IMG随Vo/Vin 的增大而减小；
（4）最高输出电压为2Vin/（k+1），当k>1 时，输出电压不能达到输入电压。
