稳态控制潮流的设定空载频率及空载电压算法

(11)形式的方程g-1个、式(8)、(12)形式的方程g个、式(13)形式的方程n个、式(14)形式的方程n个，共2g+2n-1个方程式。给定f₀V_G0潮流问题是联立求解方程式(7)、(8)、(11)~(14)以计算系统的潮流。也就是根据二次调节的设定值f₀V_G0，针对给定负荷功率、负荷阶跃扰动或网络结构的变化等，在系统输入、输出和网损功率平衡条件下，计及全系统的机组均按所设定的控制目标进行一次自动调节的结果。
3  联立求解算法
    用牛顿法联立求解方程式(7)、(8)、(11)~(14)的修正方程中，其隐极机(凸极机类似)的雅可比矩阵元素见附录。
4  算例
    为验证所提控制潮流及算法的正确、有效性， 对IEEE30节点系统^[5]，取发电机参数x_d及控制参数k_δ、k_G列于表1，根据给定发电机出力的方式^[5]，将推算的设定值f₀、V_G0也列于表1中。
    按一次自动调节规律的扰动潮流计算验证，当节点21的负荷阶跃增倍扰动、各机组按已设定的控制参数进行一次自动调节时的稳态潮流计算结果列于表2。当节点21的负荷阶跃增倍扰动时，在给定的发电机出力方式^[5]下，仅由平衡节点作功率松弛的常规潮流计算结果列于表3。

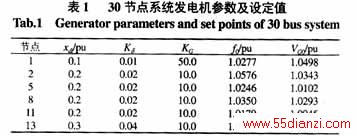
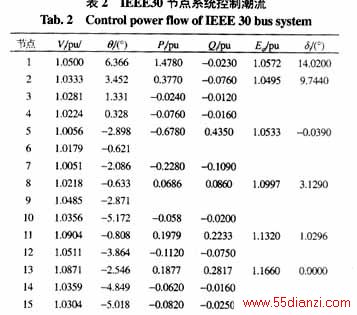
       表2说明若原设定的空载频率f₀和空载电压V_G0不变，即不作二次调节，当系统运行状况变化时，其参与一次自动调节的各机组输出功率相应作出了调整，且影响了系统电压及潮流。
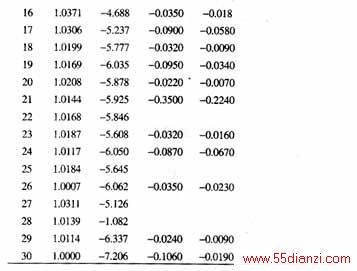
    表3是针对相同负荷扰动的常规潮流计算结果，其满足原给定的PQ、PV和平衡节点条件，但对照表1和表3中的空载频率f₀和空载电压V_G0可知，要满足给定的机组出力，各发电机组需作相关的系列二次调节。

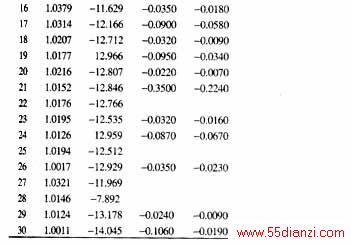
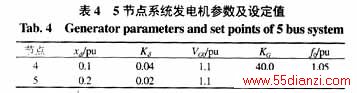
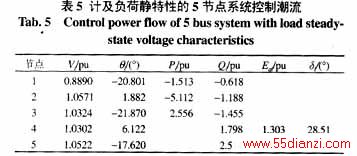
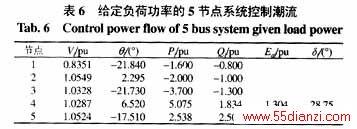
        对某一5节点系统及其负荷静特性 ^[4]进行给定f₀V_G0，确定发电机出力(P_G、Q_G、V_G)的潮流计算。电机参数及控制设定值列于表4。以V=1.0，E_q=1.05，d=0，q=0为初值进行迭代计算，计负荷静特性的结果列于表5，不计负荷静特性的计算结果列于表6。
    表5、6说明了根据给定值f₀V_G0，不须设置平衡节点，即可按机组的控制特性和节点功率平衡确定系统各节点电压和机组出力，若各机组的f₀V_G0的选择是使系统的某项指标最优，那就确定各机组的最优出力，而不是在某些电压给定下的条件最优。

5  结论
    在用于潮流计算的非线性方程组及其迭代求解的方法中，构建描述电力系统控制要求的非线性方程组也是一个重要方面，因此扩展了潮流计算在机组的控制装置均自动参与按控制方式进行调节时的潮流分析应用范围。
    利用给定f₀V_G0的控制潮流算法，可讨论控制目标f₀、V_G0和控制特性K_δ、K_G的适当设置对电力系统潮流的影响，特别是其不需平衡节点的形式，更符合全系统机组均参与按设定方式调节的实际。
    计及控制环节准稳态方程的电力系统潮流计算迭代格中，控制环节的影响在雅可比矩阵中是高度稀疏和有规律的，利用此稀疏性和规律性，可有效地解决迭代过程中的内存及计算量而不会引发维数灾问题。

上一页  [1] [2] 

本文关键字：潮流  电工技术，电工技术 - 电工技术