具有变压器分接头和补偿动作次数限制的无功优化
点击数：7474 次 录入时间：03-04 11:35:38 整理：http://www.55dianzi.com 电工技术
s进行比较，若rnd≤Ps则选择该个体，否则淘汰该个体。对于那些适应值低于平均值的个体，若rnd≥Ps则选择该个体，否则淘汰该个体。这样不仅保留了群体中那些适应值较高的个体，以利于搜寻最优值使迭代收敛，而且保留了一些“较差的”值，又保证了个体在解空间中的分散性，在一定程度上避免了“早熟”现象。由于采用的是竞争的选择策略，所以若在某代群体中有个别个体的适应值大大高于其他个体，该个体也只会入选一次，这种方法使每个个体入选的概率与适应值的大小不直接成比例，在一定程度上避免了“家族优势”。在本文中，对于该代中的最优个体不进行上述操作直接进入下一代。
2) 杂交和变异：对于杂交和变异采用了模板杂交和变异的方法，即首先随机建立一个与个体码串长度相同的二进制码串作为模板，然后依据模板上相应位置是0还是1确定是否进行杂交和变异。这样做可以使基因中的各个位得到同样的杂交和变异的机会，充分发挥每个控制变量的作用，扩大搜索范围以找到最优解。
2.3遗传算法与Alopex方法的结合
遗传算法与Alopex方法相结合的具体做法为：
在杂交算子的后面加上Alopex方法，由于Alopex方法能在产生子代的同时随机产生一定的“噪声”，使子代与父代相比有一定的差异，这样不但会使种群具有一定的多样性，也使得算法有机会跳出局部极小值，收敛到全局最优，并可以在一定程度上加快收敛速度。此外Alopex算法在搜索过程中利用了前一次自变量及其函数值的变化信息，即方向信息，将有利于缩短搜索时间，而且其“噪声”随着收敛过程的进行逐步减少也有利于优化向全局最优前进。
在未改进的Alopex方法中，自变量正向变化和反向变化的步长相等。但是在实际优化中，自变量按正方向变化时步长应该小一些，以免由于步长过大而错过最优值。而自变量向反方向变化时步长应该大一些，因为自变量向反方向变化就是为了能使目标函数摆脱局部最优值。因此，本文对Alopex方法作了一些改进，即采用了变化的步长。本文中步长δ取为
其中a，γ为常数，可根据不同的优化问题来选择合适的值。当自变量按正方向变化时步长应该小一些(0<γ≤1)，以免由于步长过大而错过最优值。而当自变量向反方向变化时步长应该大一些(γ>1)，使目标函数能够摆脱局部最优值。而且随着迭代次数的增加，步长δ越来越小也有利于收敛到最优值。
3计算步骤
1) 根据有功、无功负荷曲线和可调变压器分接头动作次数的限制，把负荷曲线划分成几个大时段。
2) 在每一个分段中，选择一个接近于该段平均负荷的典型负荷点，对该典型负荷点进行无功优化，得到相应的变压器分接头档位和补偿的投切组数。记下前N个最优解。
3) 对该段中其余的负荷点，将其变比固定为所得的最优解的变比，然后进行优化(即只进行发电机端电压和补偿的优化)。
4) 计算各负荷点的有功网损之和，在N个最优解中找出费用之和最小的解作为该段的优化解。
5) 对每一分段都进行上述计算，全天优化完毕后，计算平均的电压合格率
6) 若平均电压合格率满足要求，则优化结束。输出各时段的变压器分接头档位和补偿的投入组数。若不满足要求，则将电压合格率最低的一个分段再划分为两个时段重新进行2)、3)、4)、5)步的计算。
4算例
采用本文提出的算法对IEEE-14Bus系统进行了计算。一天负荷曲线如图1所示，电源节点的电压幅值设为0.90到1.10，负荷节点的电压幅值设为0.95到1.05，变压器变比为0.9到1.1，档距为0.0125，一天动作次数限制为6次。在补偿节点处有5组电容器和5组电抗器，每组标么值为0.1。根据负荷曲线取分段数为3，无功优化后的结果为表1所示。
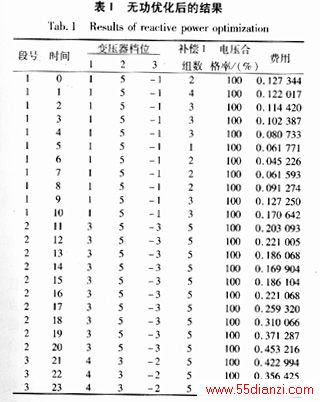从结果可知，变压器1总变化次数为3，变压器2总变化次数为2，变压器3总变化次数为3，平均电压合格率为100%，均满足要求。
5结论
本文在满足一天内变压器分接头和补偿电容动作次数约束和电压合格率的条件下，提出了对一天内负荷进行无功优化的分段算法，其中也兼顾考虑了电力市场的相关约束情况。并采用了遗传算法和Alopex方法相结合的算法进行计算。通过对算例的计算，结果说明本文提出的方法是可行的。上一页 [1] [2]
本文关键字：变压器 接头 电工技术，电工技术 - 电工技术
